Sharp EL-9900G SII
Eignung

Die NRW-Anforderungen werden erfüllt. Nach relativ kurzer Einarbeitungszeit lässt sich der EL-9900G SII weitgehend intuitiv bedienen, und zwar sowohl als normaler Taschenrechner als auch in weiteren Funktionsbereichen, speziell als Funktionenplotter.
Fazit: Der EL-9900G SII ist ein für den schulischen Einsatz brauchbarer GTR zu einem attraktiven Preis. Technisch ist er nicht unbedingt auf dem neuesten Stand, was allerdings (aus Sicht des Lehrers) den Vorteil hat, dass das Problemfeld "Spiele am GTR" eher vernachlässigt werden kann.
Hardware
Abmessungen: 91 x 186 mm
Display: 69 x 40 mm (132 x 64 px)
Gewicht: 276 g (mit Batterien)
Stromversorgung: 4x AAA (Akkus möglich)
Besonderheit: Wendetastatur
Der EL-9900G SII macht einen stabilen Eindruck und scheint ordentlich verarbeitet zu sein. Die Tasten sind angenehm in der Bedienung, die Beschriftung ist gut ablesbar. Die nominelle Auflösung des Displays kann mit den neuesten GTR zwar nicht mithalten, aber die Darstellung ist gut lesbar und ausreichend. Als besonderes Feature verfügt dieses Modell über eine Wendetastatur. Über einen Arretierhebel im Batteriefach kann die Tastatur herausgenommen und umgedreht werden. So kann man zwischen einer Tastatur für Anfänger (grün) und einer für Fortgeschrittene (blau) wählen. Technisch wirklich gut gelöst, aber praktisch unnötig. Das hat Sharp inzwischen auch selbst eingesehen und verzichtet beim optisch gelifteten Nachfolger EL-9950 darauf. Der Anfängertastatur fehlen wichtige Zugriffsmöglichkeiten (z.B. Matrizen, trigonometrische Funktionen), die sie für den Einsatz in der Oberstufe unbrauchbar macht. Dafür hat die grüne Tastatur eine Taste zur direkten Umwandlung von Bruch- und Dezimalbruchdarstellung, die der blauen Tastatur leider fehlt.
Zubehör
Der EL-9900G SII wird mit einem kompletten, fast 300 Seiten starken, gedruckten (deutschen) Handbuch ausgeliefert. Für Traditionalisten auf jeden Fall ein Pluspunkt, für die jüngere Generation eher uninteressant. Auf der anderen Seite ist man mit dem Zubehör allerdings knausrig: Um eine Verbindung zum PC herzustellen, benötigt man das "Link-Kit CE-LK4", das für etwa 25 Euro erhältlich ist und das erforderliche Kabel sowie die Software enthält. Kostenlos gibt es zumindest einen Emulator für den PC, mit dem man sich z.B. vor dem Kauf mit der Bedienung des Modells vertraut machen kann.
Bedienkonzept

Im Rechenmodus lässt sich der GTR von Sharp überwiegend intuitiv bedienen, wenn auch mit leichten Abstrichen.
Vermisst habe ich zum Beispiel eine Taste zum Wechsel zwischen Bruch- und Dezimalbruchdarstellung (nur auf
der Anfängertastatur vorhanden), die ich für den schulischen Einsatz für nahezu unentbehrlich halte.
Aufrufen kann man diese Funktion nur über die [CATALOG]-Taste, die eine alphabetisch geordnete Liste sämlicher Funktionen zur Auswahl liefert.
Glücklicherweise steht die Umwandlungsfunktion ganz oben in dieser Liste, so dass man vergleichsweise schnell darauf zugreifen kann. Wie
das aussieht, zeigt die Abbildung am Beispiel des Terms 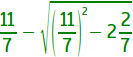 .
.
Nicht vorgesehen ist die Änderung der Bediensprache, die auf Englisch fest eingestellt ist. Das ist zwar nicht mehr Stand der Technik, aber da die meisten Zugriffe auf bestimmte Funktionalitäten ohnehin über (teils sehr kurze) Abkürzungen funktioniert, ist das kein erheblicher Mangel. Sehr ordentlich ist auf jeden Fall die „natürliche Darstellung“ von Termen, die es bei Sharp übrigens seit 2002 gibt - da waren die Mitbewerber noch nicht so weit. Problemlos funktioniert auch das Editieren vorheriger Eingabezeilen, wenn man weiß, dass man dafür die [ENTRY]-Taste benötigt, die bei jeder Betätigung eine Eingabezeile weiter zurück springt.
Details
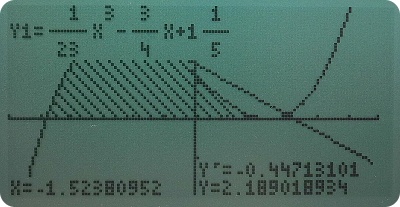
Beispiel 1:
Die Abbildung zeigt den Graphen zum Term
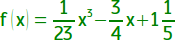 , leider im oberen Teil durch den überlagerten
Funktionsterm abgeschnitten. Positiv ist aber auf jeden Fall die natürliche Darstellung des Terms!
Nun sollte das Integral im Intervall [-4,8; 2,5] schattiert und der entsprechende Wert berechnet werden.
Bereits das Schattieren ist knifflig und ohne Handbuch nicht zu schaffen.
Einzugeben ist shade(0,y1,-4.8,2.5), wobei die Reihenfolge der Parameter strikt einzuhalten ist, damit es funktioniert.
Das heißt: Erst der Term mit den kleineren y-Werten, dann der mit den größeren, danach die Integrationsgrenzen.
Dann wird zwar schattiert, allerdings nichts berechnet!
Um den Wert des Integrals zu erhalten, muss über die Taste [MATH] das Menü für mathematische Berechnungen geöffnet und dort
dann [CALC][∫] ausgewählt werden. In der sich öffnenden Maske gibt man die Grenzen ein und den Integranden.
Das wiederum führt zunächst zu einer Fehlermeldung, weil das abschließende Differential dx fehlt! Dieses muss manuell ergänzt werden
über die Tasten- bzw. Menüfolge [MATH][CALC][dx]. - Sehr umständlich! Das funktioniert bei Geräten anderer Hersteller deutlich eleganter.
, leider im oberen Teil durch den überlagerten
Funktionsterm abgeschnitten. Positiv ist aber auf jeden Fall die natürliche Darstellung des Terms!
Nun sollte das Integral im Intervall [-4,8; 2,5] schattiert und der entsprechende Wert berechnet werden.
Bereits das Schattieren ist knifflig und ohne Handbuch nicht zu schaffen.
Einzugeben ist shade(0,y1,-4.8,2.5), wobei die Reihenfolge der Parameter strikt einzuhalten ist, damit es funktioniert.
Das heißt: Erst der Term mit den kleineren y-Werten, dann der mit den größeren, danach die Integrationsgrenzen.
Dann wird zwar schattiert, allerdings nichts berechnet!
Um den Wert des Integrals zu erhalten, muss über die Taste [MATH] das Menü für mathematische Berechnungen geöffnet und dort
dann [CALC][∫] ausgewählt werden. In der sich öffnenden Maske gibt man die Grenzen ein und den Integranden.
Das wiederum führt zunächst zu einer Fehlermeldung, weil das abschließende Differential dx fehlt! Dieses muss manuell ergänzt werden
über die Tasten- bzw. Menüfolge [MATH][CALC][dx]. - Sehr umständlich! Das funktioniert bei Geräten anderer Hersteller deutlich eleganter.
Beispiel 2: Das Zeichnen einer Wendetangente geht mit dem EL-9900G S II in wenigen Schritten und lässt die gesamte Konkurrenz alt aussehen. Nach dem Zeichnen des Graphen bestimmt man über [CALC][Inflec] den Wendepunkt, der Trace-Cursor springt zu dieser Stelle. Anschließend drückt man [CALC][Draw][T_line] und [ENTER] - das war's. Die Tangente wird gezeichnet und die Gleichung zusätzlich eingeblendet. ABER: Der ermittelte Wendepunkte W(0.01339|1.18996) ist viel zu ungenau - der richtige Wendepunkt ist W(0|1.2). Dies hat natürlich zur Folge, dass auch die Koeffizienten der Tangentengleichung fehlerhaft sind.
Beispiel 3:
Die Berechnung des Integrals 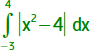 liefert nach
einigen Sekunden Rechenzeit als Ergebnis 23.66667239. Die Abweichung vom exakten Wert 23 ⅔ kommt dadurch zustande,
dass die Genauigkeit auf 10-5 voreingestellt ist. Zwar lässt sich diese Voreinstellung nicht ändern, wohl aber
für jeden Einzelfall die Genauigkeit festlegen, indem man rechts des Integranden vor dem dx durch Komma getrennt
die einzuhaltende Toleranz angibt. Setzt man diesen Wert auf 10-10, dann ist der berechnete dezimale Näherungswert so
genau, dass mittels [→a␣b/c]-Funktion tatsächlich 23 ⅔ herauskommt. Problem dabei:
Die explizite Angabe der Toleranz ist umständlich, zerstört die mathematisch korrekte „natürliche Darstellung“ und ist insbesondere
nicht intuitiv erfassbar, d.h. für den schulischen Einsatz kaum praktikabel.
liefert nach
einigen Sekunden Rechenzeit als Ergebnis 23.66667239. Die Abweichung vom exakten Wert 23 ⅔ kommt dadurch zustande,
dass die Genauigkeit auf 10-5 voreingestellt ist. Zwar lässt sich diese Voreinstellung nicht ändern, wohl aber
für jeden Einzelfall die Genauigkeit festlegen, indem man rechts des Integranden vor dem dx durch Komma getrennt
die einzuhaltende Toleranz angibt. Setzt man diesen Wert auf 10-10, dann ist der berechnete dezimale Näherungswert so
genau, dass mittels [→a␣b/c]-Funktion tatsächlich 23 ⅔ herauskommt. Problem dabei:
Die explizite Angabe der Toleranz ist umständlich, zerstört die mathematisch korrekte „natürliche Darstellung“ und ist insbesondere
nicht intuitiv erfassbar, d.h. für den schulischen Einsatz kaum praktikabel.
Beispiel 4: Zum Lösen eines LGS kann man über [TOOL][SYSTEM] die Koeffizienten in eine vorbereitete Maske eingeben. Das funktioniert problemlos, wenn man weiß, dass man zum Lösen danach [2ndF][EXE] statt [ENTER] drücken muss und wenn das LGS eindeutig lösbar ist. Ansonsten wird man nämlich mit der Meldung "ERROR 02" stehen gelassen, und zwar unabhängig davon, ob das LGS keine oder mehr als eine Lösung hat. Mit diesem Verhalten befindet sich der EL-9900G S II zwar in guter Gesellschaft, aber anwenderfreundlich ist es dennoch nicht.
Empfehlenswert ist es darum, zum Lösen eines LGS die Matrizen-Variante zu wählen. Die funktioniert immer, hat allerdings den Nachteil der umständlicheren, wahrlich nicht intuitiven Bedienung. Dazu wird zunächst über [MATRIX][EDIT][mat A] eine Matrix ausgewählt, die entsprechend zu dimensionieren und zu befüllen ist. Danach muss man in den normalen Rechenmodus wechseln, um die Matrix mittels [MATRIX][MATH][rrowEF] [MATRIX][NAME][mat A][ENTER] in reduzierte Zeilenstufenform ("normierte Diagonalform") zu überführen.
Für beide Varianten gilt gleichermaßen: Brüche können zwar eingegeben werden, sie erscheinen allerdings nur in der klassischen "a⌟b"-Darstellung auf dem Display. Und: Ergebnisse erscheinen immer als Dezimalbrüche ohne Möglichkeit der Umwandlung in einen Bruch.